Without a doubt, Mathematics is the highest scaling course in the HSC, being an average level student in one of the Mathematics Extension courses can boost your final ATAR significantly. Quite frankly, having Mathematics as one of your subjects provides you with an ‘unfair advantage’. However if this is true, why is it that so many students decide to forego choosing Mathematics as one of their subjects? Or why some students still fail to achieve their goal ATAR, despite having done mathematics? The answer is quite simply that Mathematics can be damn hard sometimes, and finding success in this subject is difficult. However believe me when I say that you don’t need to be some genius to succeed in Mathematics, in fact I know of numerous average intellect students who have been able to find success in all levels of mathematics. All that is required of you is discipline, patience, determination and good exam technique.

 This article will discuss:

• Why choose Mathematics as a subject? 
• What level of Mathematics should I study? 
• How can I improve my marks and eliminate careless mistakes?
• Advanced Mathematics 
• Extension 1 
• Extension 2 
• Final Tips 

Note: This is a very comprehensive article, so use the above guide to read the content that is relevant to you.

Why choose Mathematics as a subject?

Firstly I will go ahead and say that Mathematics is not for everyone. Always play to your strengths and hide your weaknesses. So if you are a student who truly struggles with numbers, then it would be unwise to choose this subject. However if you have always been average at math, and are sitting on the fence about whether to do it or not, then here are some points that may help you make your decision.

1. There are no essays, no techniques, no quotes, no historical dates, and no statistical figures that need to be memorized. In fact I would go, as far as to say that there is practically nothing is Math that needs to be memorized. Everything, every formulae, every method can be understood and made to be a part of your common sense.
2. Everything is connected. Mathematics is logical and intuitive, and so extremely easy to study for. As long as you have done your homework, there is no need to cram for exams.
3. No essays, no assignments in Mathematics. Just perform well in your exams and you are set.

What Level of Mathematics should I study?

In making this decision, you need to consider both your own ability in Mathematics and the relative scaling of each subject.

The following data has been drawn from numerous ATAR calculators:

The Mathematics Extension courses are the highest scaling subjects in the HSC, and thus can provide you with a huge advantage over your competition. Here are some statistics to make this more concrete.

To achieve an ATAR of 99, you would need to be:

• Average in Ext 2 Mathematics.
• In the top 25% of Ext 1 Mathematics.
• In the top 3% of Advanced Mathematics.

To achieve an ATAR of 97, you would need to be:

• In the top 80% of Ext 2 Mathematics, i.e. if there where 10 students, you would only need to come 8^th.
• Average in Ext 1 Mathematics.
• In the top 10% of Advanced Mathematics.

To Achieve an ATAR of 90, you would need to be:

• Just around last in Ext 2 Mathematics, and be able to attain a mark of around 65%.
• In the top 75% of Ext 1 Mathematics.
• In the top 40% of Advanced Mathematics.

Hence it is obvious that Extension 1 & 2 Mathematics are a must if you are good at Math. You could be far below average in these courses and still easily be on track to getting an above 90 ATAR.

However what the above data also shows is that the Advanced Mathematics course itself is extremely good. Say you had an ATAR goal of around 80 to 85. Mathematics could easily be your best subject, and drag your final ATAR to the high 80s or low 90s, while at the same time requiring minimal effort compared to the larger amounts of energy you would need to be expending into the humanities or English based subjects.

How can I improve my marks and eliminate careless mistakes?

While students with a natural talent for Mathematics will generally perform well, let me stress to you all again that an extremely average student can perform just as well, with the proper study technique and correct exam technique. Here are three of the things that worked for me, and which I believe can work for any student, regardless of natural ability, as long as they have the patience and determination to stick with it.

1. Understand, not memorize.

Foundations are important. You might be able to recite the most complicated aspects of the course. But when pressure hits and the exam clock’s ticking away, you’ll realize you don’t know how to apply your knowledge.

Possibly the most important (but also most frustrating), part of preparing for a Math exam is understanding all the formulae in the course. ‘Understanding’ is more than just memorizing. Understanding means to know when and where to apply different formulae and being able to do so without making mistakes.

This understanding can be built through repeated practice. Practice gives meaning to your formulae and will make it clear when and how to apply the formula in different situations. Basically the more practice questions and past papers you do, the greater understanding you will have of your formulae and eventually the process of answering questions will become automatic for you.

Additionally as mentioned above, mathematics is a logical subject. Thus it is often helpful to not only know a formula, but to also understand how it is derived. When you can see the logic behind a formula, then it will be much easier to understand and remember. 

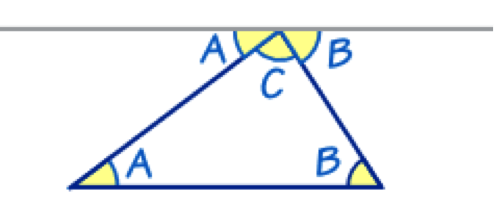
Example: Why the interior angle sum of a triangle is 180 degrees.

This is a proof that the angles in a triangle equal 180°:

The top line (that touches the top of the triangle) is
running parallel to the base of the triangle.

So:

• angles Aare the same
• angles Bare the same

And you can easily see that A + C + B does a complete rotation from one side of the straight line to the other, or 180°

2. Challenge yourself and make a lot of mistakes

Funnily enough the best way to lessen the amount of mistakes you make during assessments is to make a ton of them during practice. This may sound strange, but making mistakes when the marks don’t count can really help ensure you won’t do the same when the marks do count.

Benefits of making mistakes during practice:

• It helps you understand how not to do a question, so if you encounter the same type of question again in an exam, you will already know what method not to use.
• It helps you understand more than one way to do a question.
• It helps you find the topics you are weaker at, and also the gaps in your knowledge.
• Using the wrong method may not help you solve a question, but it isn’t a waste of time, because you are still spending time practicing other methods.

However it is obvious that you won’t be making many mistakes unless you are challenging yourself and pushing yourself to try questions, which you may not have encountered before. Many students prefer to stay within their comfort zone and are afraid to try harder questions for the fear of seeming dumb. However I promise you that if you step outside your comfort zone in tackling these more complex questions, you will have no regrets. Every question, whether it takes you a day, or a week to solve will never be a waste of time. It will always help you gain a lot of experience about what method to use, in different situations, whilst also boosting your confidence in you problem solving ability.

3. Set out your work properly

This may be the simplest, yet most effective way to improve your marks and eliminate careless mistakes. Unfortunately I have seen very few fellow peers and students being able to do this simple task. So read the next couple of paragraphs carefully as they will help you add 5-10 marks to your next exam with minimal effort.

Just as structuring your English or History essays into paragraphs is important, structuring your working out clearly in mathematics is important.

Clear setting out helps you:

• Avoid making careless mistakes in the first place
• Give your examiner a clear picture of the logic and flow of your reasoning
• Solve more complex questions
• Check your work for mistakes more efficiently

If you are one of those people who keep on making a ton of careless mistakes, you should avoid skipping steps. Spend the time to write those few extra lines, and avoid giving away cheap marks. Also remember, even if your answer is wrong, most of the time the examiner will award you marks just for your working out.

Some simple tips to make your proofs clearer:

1. Clearly explain what the variables you introduce mean, by either indicating clearly on a diagram or by writing at the top of your proof:

Let x be the…

2. Don’t skip steps and more is always better
   1. If you are unsure whether or not you need to include a certain bit of information, INCLUDE IT! Always explain your reasoning as if you were explaining it to someone who didn’t know mathematics.

3. Draw big diagrams and clearly label them
   1. This may seem trivial, but having a large diagram, which is detailed, allows you to see things more clearly. For example in geometry questions, a larger diagram allows you to mark in angles and important features more accurately.

In the following 3 sections I will provide a description of each of the mathematics courses and how an average student should perform. There will also be a brief breakdown of each of the final exams to give you a general idea of what you will be in for, depending on what subject/s you decide to take.

Advanced Mathematics:

In terms of difficulty the Advanced Mathematics course is not much harder than the General Mathematics course, but scales much better. Thus I would always encourage you to attempt the ‘advanced’ course even if you feel math is not your strongest suit.

Brief Snapshot of the HSC Exam:

Since 2012, the final HSC Advanced Mathematics Exam consists of:

Section 1:

10 multiple-choice questions (Questions 1-10)

• These questions are fairly straightforward and can come from any of the 2u topics.
• Any average student should be aiming for at least an 8/10 in this section.
• Maximum of 20 minutes should be spent on these questions

Section 2:

6 extended problem-solving question. (Questions 11-16)

Questions 11/12/13: (Easy/Medium) (1 hour)

The first three questions are simple and straightforward. They are pretty much the type of questions that your teachers would have set you from the textbook. The topics usually tested in these three questions are:

• Basic Arithmetic and Algebra
• Plane Geometry
• Trigonometry
• Some simple probability
• Some simple calculus

What an average student should aim for:

Since these questions are standard, an average student should be aiming for 95% in this section. By the time you reach October, the types of problems tested in this section should be second nature. It is important not to forfeit any marks to careless errors in the first parts of the exam, as the questions get progressively harder and you will almost definitely find questions you cannot do in the latter parts.

Questions 14/15 (Medium) (50 minutes)

The next two question contain other topics from the course, including:

• Quadratic Polynomial & the Parabola
• Geometric Applications of the Derivative
• Series and Applications
• Harder Integration

What an average student should aim for:

Though these questions are harder, they are still just testing the standard content from more complex topics. Thus in this section the average student should be aiming to score around 80%. So that overall they should have scored around 76 of the 85 marks and have completed it in about 2 hours and 10 minutes, leaving enough time remaining for a good attack on the last three questions.

Question 16 (Hard) (50 minutes)

The last question of this exam is mainly used to separate the state rankers from the rest of the cohort, so don’t worry too much about getting full marks in this section. If you can get around 60-70% of the marks in this question you will have already done well enough to be above average. This section mainly consists of problems, which are extended into many separate parts.

Some tips for scoring easy marks in this section:

• The problems are usually separated into easy and hard components. Doing all the easy components can snag you a couple of easy marks with minimal effort.
• Clearly set out your work, remember markers may award you points for correct reasoning, even if you don’t get the final answer.

What an average student should aim for:

Getting around 70% in this section, would leave you with a final mark around 87/100. This has an ATAR equivalent of 91.8. Whilst getting the same mark in General Mathematics would lead to an ATAR of 85.6.

Extension 1 Mathematics:

In terms of difficulty the 3u course builds on from the 2u course and also involves a few new and more complex topics. This means that any content that is covered in the 2u course may also be tested in the 3u exam. This course scales substantially better than the Advanced Mathematics course, but again your decision to do a subject should be based on a consideration of both your ability and the scaling of a subject. I would recommend this course to students who are above average in the preliminary courses.

Brief Snapshot of the HSC Exam:

Since 2012, the final HSC Advanced Mathematics Exam consists of:

Section 1:

10 multiple-choice questions (Questions 1-10)

• These questions are fairly straightforward and can come from any of the 2u/3u topics.
• Any average student should be aiming for at least an 8/10 in this section.
• Maximum of 20 minutes should be spent on these questions

Section 2:

4 extended problem-solving questions. (Questions 11-14)

Questions 11/12 (Easy/Medium) (40 minutes)

Like the first three questions of the 2u exam, the first two questions of the 3u exam, are fairly standard questions. They will be very similar to the questions from your textbook, and so will not require much creative thinking.

The topics often tested in these two sections are:

• Applications of Calculus
• Trigonometric Functions
• Polynomials
• The Parabola

What an average student should aim for:

Despite this being a harder course, the aim should still be to get around 95% in the first two questions. These questions are all very standard, and so should be second nature by the time you reach the exam.

Question 13 (Medium) (25 minutes)

This question will require students to be more creative in their approach to solving questions and will not be like the standard questions you see in the textbook.

Topics usually tested in this section:

• Inverse Functions
• Integration
• Further Applications of Calculus

What an average student should aim for:

Aim for around 75% in this section, i.e. 11 out of the 15 possible marks. So that overall you would have scored around 47 of the 55 possible marks thus far. This section should have been done by the 1 hour and 25 minute mark, leaving ample time to attack the final question.

Question 14 (Hard) (35 minutes)

Again the last question is mainly used the separate the state rankers from the rest of the cohort, so don’t be too focused on attaining 100% in this section.

Topics usually tested in this section:

• The geometry of a circle
• The Binomial Theorem
• Permutations and Combinations
• Projectile and Simple Harmonic Motion

What an average student should aim for:

If you could score about 8 of the possible 15 marks in this question, you have done extremely well. This would leave you with a mark of 79.6% overall. This may seem low, but it has an ATAR equivalent of 92.25.

Extension 2 Mathematics:

This exam is arguably the hardest high school mathematics paper in Australia. While considerable mathematical ability may be required to score the top marks, with the right approach even average students can achieve a strong result. To recap the lop-sided scaling advantage this course has, I will remind you of the following:

“A score of around 70% in this exam, which in reality is a high Band E3 or Band E4, will give you a scaled score equivalent to the top 4% of students in Physics, Chemistry, Economics and English, and put you well on track for a 97+ ATAR.”

Brief Snapshot of the HSC Exam:

Since 2012, the final HSC Advanced Mathematics Exam consists of:

Section 1:

10 multiple-choice questions (Questions 1-10)

• These questions are fairly straightforward and can come from any of the 2u/3u/4u topics.
• Any average student should be aiming for at least an 8/10 in this section.
• Maximum of 15 minutes should be spent on these questions

Section 2:

6 extended problem-solving question. (Questions 11-16)

Questions 11/12 (Easy/Medium) (45 minutes)

Like the two previous courses, the first two questions are again simple and straightforward. The questions are standard and there will be nothing you have not done in class.

Topics usually tested in this section:

• Integration
• Complex Numbers

What the average student is aiming for:

Like I mentioned earlier, it is important not to forfeit any marks to careless errors in the first parts of the exams as the question get progressively harder and you will almost definitely find questions you cannot do in the latter parts. Since these questions are standard you should be aiming for around a 25/30.

Questions 13/14 (Medium/Hard) (50 minutes)

These questions though more difficult, are still assessing the standard content of each of these topics and are fairly accessible to students who have a good grounding in each of the 4u topics.

Topics usually tested in this section:

• Curve Sketching
• Polynomials
• Conics
• Mechanics

What the average student is aiming for:

An average student should be aiming to score around 75-80% of the marks in these two questions. This would leave you on a score of around 59 of the possible 70 marks thus far.

Question 15/16 (Hard/Extremely Hard) (1 hour and 10 minutes)

These final two questions are notoriously hard, and are designed to challenge even the top students. They are usually made up of long multi-stepped problems. However do not be discouraged! If you have done the first questions well enough, and can even score half of the marks in the last two questions, you are on track for a top band performance.

Topics usually tested in this section:

• Harder 3u topics
  • Circle Geometry
  • Mathematical Induction
  • Inequalities
  • Probability

Tips to score marks in these two questions:

• Often the first part of a question is extremely long winded, but the second part is simple and only requires you do use what was given to you in the first question
  • Example: Use the result in (a), and hence deduce… in part (b)
  • Thus you can easily scavenge a few marks by just doing part (b)
• Attempt every question, even if you can’t get out the final answer, if you have made significant progress in your working out, the examiner will have to award you marks

Scoring around 50% in these two questions will leave you with a final mark of around 74/100. ATAR equivalent = 97+.

Final Tips:

This has been a long article, but I will finish off with some final tips:

1. Do all your homework
   1. This may seem trivial, but doing this can ensure you will be very familiar with all the concepts and questions that you could be tested on in your exams.
2. Perfect Practice make Perfect
   1. A lot of students do past papers. But it is only through doing them under exam conditions that you can score the best marks and really improve your exam technique.
3. Be persistent and don’t give up
   1. Always try to solve a question independently, and refrain from asking for assistance until all means have been exhausted. Remember this is never a waste of time. Through making mistakes, you learn how not to do a question and also get to practice using other methods.
   2. Plus there is nothing that builds confidence more, than figuring out a question all by yourself, after spending a whole day on it.

Looking forward to working on the whiteboards with you in 2015!

Harrison Chen

Senior Coach at HSC CoWorks